Tačka i prava

26/02/2014 15:34
Tačka
 
Najprije ćemo se upoznati sa osnovnim formulama i njihovom primjenom. 
 
1. Rastojanje između dvije tačke 
 
Ako su nam date tačke  A(x1, y1) i B(x1, y1) onda rastojanje između njih računamo po formuli 
 
d(A,B) = korijen iz (x1 - x2)" + (y1 - y2)"
 
2. Dijeljenje duži u datoj razmjeri
 
Ako je tačka M(x1, y1) unutrašnja tačka duži AB, gde je A(x1 ,y1 ) i B(x2 ,y2 ) i ako je data razmjera AM:MB = λ , u kojoj tačka M deli duž AB , onda se koordinate tačke M računaju po zadanim obrascima. 
 
 
 
Prava

Aksiomi prave

  1. Svake dvije različite tačke pripadaju jednoj i samo jednoj pravoj
  2. Svaka prava sadrži najmanje dvije zajedničke tačke.
  3. Postoje tri nekolinearne tačke

Dvije tačke su uvijek kolinearne.

Presjek dvije prave

Za dvije prave koje imaju jednu zajedničku tačku kažemo da se sijeku. Zajednička tačka te dvije prave naziva se sjecište ili presječna tačka. a ∩ b={C}

Kolinearne i nekolinearne tačke

Za tačke koje leže na jednoj pravoj kažemo da su kolinearne tačke. Za tri tačke koje ne leže na jednoj pravoj kažemo da su nekolinearne. Postoje tri nekolinearne tačke

Posljedice

1.Dvije različite prave imaju najviše jednu zajedničku tačku

2.Van svake dvije prave postoji bar jedna tačka.

Paralelne i mimoilazne prave

Za dvije prave koje leže u jednoj ravni i nemaju zajedničkih tačaka kažemo da su paralelne. Za prave koje ne leže u jednoj ravni kažemo da su mimoilazne.


Za dvije prave a i b važi:

  1. Ako je a ∩ b={A,B}=> a=b
  2. Ako je a ∩ b={A} sijeku se
  3. Ako a i b nemaju zajedničkih tačaka a ║ b

Udaljenost paralelnih pravi

Neka je data tačka M jedne prave i njena projekcije M' na drugu pravu Traži se njena projekcija


M' = B + k\overrightarrow{v}, k \in R\;\land\; AA' \bot v.

Iz navedenih uslova određujemo koeficijent k, а sа njime određenoje i M'. Udaljenost tačaka M i M' je јеdnaka udaljenosti između paralelnih pravi a i b.
 

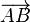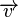U trodimenzionalnom prostoru ova udaljenost je jednaka visini paralelograma kojeg čine vektori \overrightarrow{AB} i \overrightarrow{v}. , a dobije se kao količnik površine ovog paralelograma (intenzitet vektorskog proizvoda) i intenzitet vektora v.

d(a,b) = \frac{|\overrightarrow{AB} \times \overrightarrow{v}|}{|\overrightarrow{v}|}

Udaljenost mimoilaznih pravi

Da bi se odredila udaljenost dvije mimoilazne prave treba predstaviti vektor između njih, a zatim da se odrede parametri za koje će on biti minimalan. Neka je ovaj vektor w, a opšte tačke pravih a i b su M i N.odnosno biće:
 

M = A + \alpha v = (A_1+\alpha v_1, A_2+\alpha v_2,...,A_n+ \alpha v_n), \alpha \in R N = B + \beta u, \beta \in R
 

intenzitet vektora 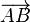\overrightarrow{AB} je |\overrightarrow{AB}| = f(\alpha,\beta) = \sqrt{(A_1+\alpha v_1- B_1-\beta u_1)^2 + \dots + (A_n+\alpha v_n- B_n-\beta u_n)^2 }. Ovdje korijen ne utiče na vrijednost na koju parametri i α i β imaju za maximalnu vrijednost izraza korijen se može izbaciti. Sada ćemo odrediti prve izvode izraza f(\alpha,\beta) pо α i po β. Dobijamo sistem dvije jednačine sa dvije nepoznate α i β, koji možemo riješiti.
 

\begin{cases} f(\alpha,\beta)'_\alpha \\ f(\alpha,\beta)'_\beta \end{cases}
 

Određujemo α и β i vrijednosti uvrstimo u jednačine prave a i b, Ove koordinate će predstavljati tačke, nazovimo ih 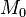M_0 i N_0, d(a,b) = d(M_0,N_0).
 

Aksiom uređenosti prave

Prava je na određen način uređen skup

1.Za tačke X,Y prave a važi X <Y ili Y<X (potpunost)

2.Ako je X <Y onda nije Y<X (antisimetričnost)

 

3.Ako je (X<Y) i( Y<Z) =>X<Z (tranzitivnost)

4.Za tačku Y prave a postoje tačke X i Z na a tako da je X<Y i Y<Z( produžavanje prave)

5.Za X i Z prave a postoji tačka Y takva da je X <Y( gusto uređen skup)

 

Dedekindov aksiom

Ako sve tačke prave podijelimo u dvije neprazne klase tako da je svaka klasa prve klase ispred svake tačke druge klase onda ili prva klasa ima svoju poslednju ili druga klasa svoju prvu tačku

Ravan

Ravan je određena sa aksiomama.


Aksiomi ravni

  1. Svake tri nekolinearne tačke pripadaju jednoj i samo jednoj ravni.
  2. Svaka ravan sadrži najmanje tri nekolinearne tačke.
  3. Postoje 4 tačke koje ne pripadaju jednoj ravni

Komplanarne i nekomplanarne tačke

Za tačke koje leže u jednoj ravni kažemo da su komplanarne. Za 4 tačke koje ne leže u jednoj ravni kažemo da su nekomplanarne.

Aksiom prave i ravni

Ako ravan sadrži dvije različite tačke jedne prave onda ona sadrži tu pravu.

Posljedica

Ravan i prava koja ne leži u toj ravni mogu imati najviše jednu zajedničku

Teoreme o određenosti ravni

Teorema 1

Postoji jedna i samo jedna ravan koja sadrži dvije prave koje se sijeku.

Teorema 2

Postoji jedna i samo jedna ravan koja sadrži datu pravu i datu tačku koja ne pripada toj pravoj.

Teorma 3

Postoji jedna i samo jedna ravan koja sadrži dvije paralelne prave

Aksiom dviju ravni

Presjek dviju različitih ravni je prava.

Međusobni položaj prave i ravni

a i α imaju bar dvije zajedničke tačke, onda a leži u α

a i α imaju jednu zajedničke tačke, onda prava a siječe ravan α


a i α nemaju zajedničkih tačaka, onda je prava a paralelna sa ravni α

 
i) opšti ( implicitni oblik) je ax + by+ c = 0 
ii) eksplicitni oblik je y = kx + n 
 
Ovaj oblik nam je najbitniji jer se koristi u mnogim formulama. U njemu je : 
 
k- koeficijent pravca ( k tg = α , gde je α ugao koji prava gradi sa pozitivnim smjerom x – ose) 
 
n - je odsječak na y - osi
 
x/m + y/n = 1 je segmentni oblik 
 
m – je odsečak na x osi
n – je odsečak na y osi
 

 

Back